恋上数据结构笔记:复杂度
什么是算法?
算法理解起来其实非常简单,就是是用于解决特定问题的一系列的执行步骤。
// 计算 a 跟 b 的和
public static int plus(int a, int b ) {
return a + b;
}上面的代码很简单,但是它其实也是一个算法,因为它解决了加法运算。
// 计算 1 + 2 +3 ... +n 的和
public static int sum(int n ) {
int result =0;
for (int i = 1; i <= n; i++) {
result += i
}
return result;
}sum 也是一个算法,它解决了从 1 加到 n 的问题,这两个我们都可以称之为算法,算法其实就是你能解决问题就可以了,小到一行代码,大到上万行都可以称之为算法。
但是当我们使用不同额算法,解决同一个问题,有时效率可能相差非常大。因为我们都知道当我们解决一个问题的时候,解决方案可能会有很多,写代码也是如此,不同算法之间执行效率可能会相差很多。
public static int sum2(int n) {
return (1 + n) * n / 2;
}就拿上面从 1 到 n 计算累加的算法,其实让我们如果使用数学公式解决的话,一行代码就搞定了,根本不需要使用循环。
再举个例子:求第 n 个斐波拉切(fibonacci number)
求斐波拉切的方式有很多,在这里我们用两种方案来实现:
- 递归
public static int fib(int n) {
if (n <= 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
}这是一种解决方案,肯定能够解决我们的问题,但是这个算法有性能问题,当我们把 n 写成 64 的时候,这个算法的执行效率就开始降低了,需要执行很久才能够返回。原因我们在后面说,我们先来换一个算法。
- 动态规划
我们将斐波拉切数列展开:
0 1 1 2 3 5 8 13 ....我们发现,其实最终值就是前两个值加在一起,那么我们完全可以将前面的值保存起来。
public staitc int fib (int n) {
if (n <= 1) {
return n;
}
int first = 0;
int second = 1;
for (int i =0; i < n - 1; i++ ) {
int sum = first + second;
first = second;
second = sum;
}
return second;
}当我们使用 fib(64) 的时候几乎是秒出结果。
这也就证明了,当我们以后解决问题的时候会有很多种算法,但是算法之间效率相差非常大。这两个算法的差距我们该如何测量呢?
我们可以计算它们给出结果花费时间。
package com.mj;
import java.text.SimpleDateFormat;
import java.util.Date;
public class Times {
private static final SimpleDateFormat fmt = new SimpleDateFormat("HH:mm:ss.SSS");
public interface Task {
void execute();
}
public static void test(String title, Task task) {
if (task == null) return;
title = (title == null) ? "" : ("【" + title + "】");
System.out.println(title);
System.out.println("开始:" + fmt.format(new Date()));
long begin = System.currentTimeMillis();
task.execute();
long end = System.currentTimeMillis();
System.out.println("结束:" + fmt.format(new Date()));
double delta = (end - begin) / 1000.0;
System.out.println("耗时:" + delta + "秒");
System.out.println("-------------------------------------");
}
}Times 其实就是一个代理,它可以执行满足 Task 的接口的类,然后在执行前后加入时间计数。这样我们就可以统计算法的执行时长了
int = 45
TimeTool.check("fib1", new Task() {
public void execute() {
System.out.println(fib1(n));
}
});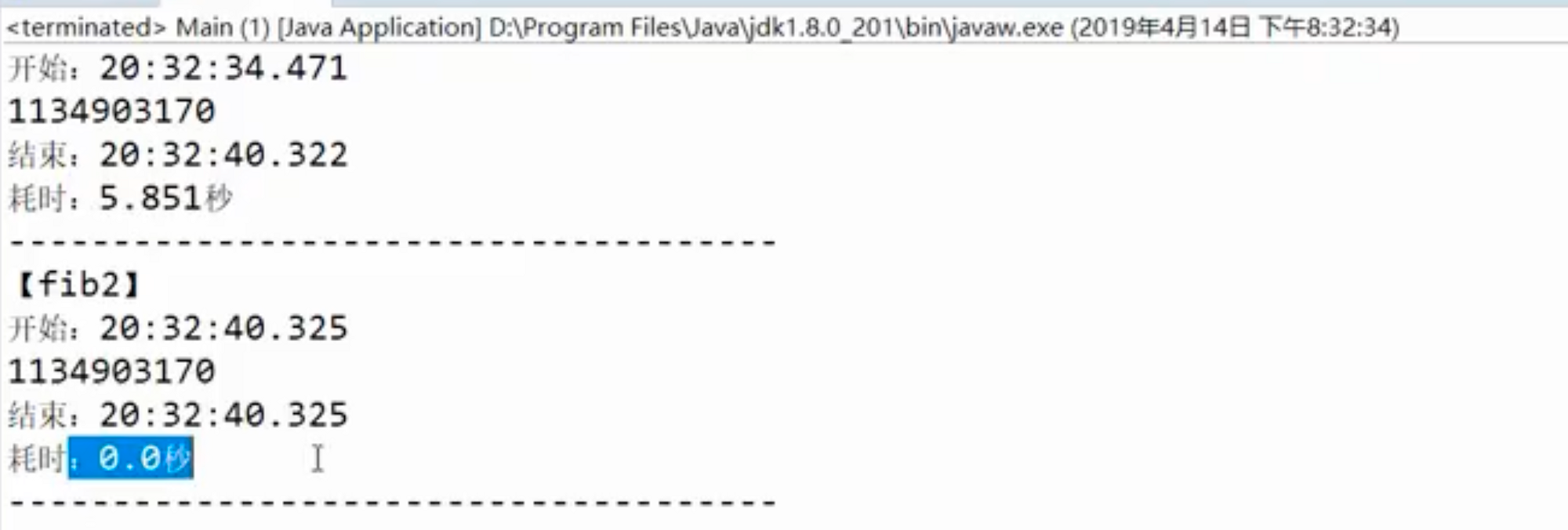
我们对比两个算法之间的差距,可以发现采用动态规划的的方案,随着数字的增大执行时间并不是很大,但是采用递归的方案,时间就慢慢的增加了。

当我们执行 n = 46 的时候,采用递归的方案时间已经达到了 9.44 秒。
如何评判算法的好坏?
还是拿上面的两个案例来举例,我们可以拿代码越短就证明代码越好吗?
肯定不行,在累加中的确是利用公式更好,因为它代码足够简洁,但是在斐波拉切中,反倒是代码更多的执行效率更好。
如果单从执行效率上进行评估,你可能会得到这么一个方案,比较不同算法对同一组输入的执行处理时间这种方案也叫做:事后统计法。
但是这种方案是有以下缺点:
- 执行时间严重依赖硬件以及运行时各种不确定的因素环境,例如 CPU 更好,当前进程数量比较少等等。
- 必须编写相应的测试代码
- 测试数据的选择比较难保证公正性
一般从以下维度来评估算法的优劣
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
- 时间复杂性(time complexity):估算程序指令的执行次数(执行时间)
- 空间复杂度(space complexity):估算所需占用的存储空间
算法的评估
我们来算一下面这个函数需要执行多少条指令
public static void test1(int n) {
// 汇编指令
// 1
if (n > 10) {
System.out.println("n > 10");
} else if (n > 5) { // 2
System.out.println("n > 5");
} else {
System.out.println("n <= 5");
}
// 1 + 4 + 4 + 4
for (int i = 0; i < 4; i++) {
System.out.println("test");
}
// 140000
// O(1) 时间复杂度
// O(1) 空间复杂度
}判断的执行指令次数我们假定是 1,这样算其实不太严谨,但是没有关系,我们先按照这个规则计算。
我们继续向下,到了 for 循环的时候 int i = 0,我们算一个指令,i++ 会执行 4 次,i < 4 会被执行 4 次,for 循环中的打印输出也会执行四次,这样就是 1 + 4 + 4+ 4。总的算下来 就是14。
public static void test2(int n) {
// O(n)
// 1 + 3n
for (int i = 0; i < n; i++) {
System.out.println("test");
}
}int = 0 是 1 次, i < n 执行 n 次, i++ 执行 n 次,输出执行 n 次,那么执行指令的次数就是 1 + 3 * n 次。
public static void test3(int n) {
// 1 + 2n + n * (1 + 3n)
// 1 + 2n + n + 3n^2
// 3n^2 + 3n + 1
// O(n^2)
// O(n)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
}
public static void test5(int n) {
// 8 = 2^3
// 16 = 2^4
// 3 = log2(8)
// 4 = log2(16)
// 执行次数 = log2(n)
// O(logn)
while ((n = n / 2) > 0) {
System.out.println("test");
}
}
public static void test6(int n) {
// log5(n)
// O(logn)
while ((n = n / 5) > 0) {
System.out.println("test");
}
}
public static void test7(int n) {
// 1 + 2*log2(n) + log2(n) * (1 + 3n)
// 1 + 3*log2(n) + 2 * nlog2(n)
// O(nlogn)
for (int i = 1; i < n; i = i * 2) {
// 1 + 3n
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
}
public static void test10(int n) {
// O(n)
int a = 10;
int b = 20;
int c = a + b;
int[] array = new int[n];
for (int i = 0; i < array.length; i++) {
System.out.println(array[i] + c);
}
}上面的这些函数计算方式都差不多,我就直接列在这里了。
大 O 表示法
我们已经算出了执行指令的大概次数,但是看上去还是很复杂。这个时候我们就要用大 O 表示法来描述复杂度,它表示的是数据规模 N 的一应的复杂度。
规则如下:
忽略常数、系数、低阶
- 9 >> O(1)
- 2n + 3 >> O(n)
- n^2 + 2n + 6 >> o(n^2)
- 4n^3 + 3n^2 + 22n + 100 >> o(n^3)
上一节中的函数对应的大 O 表示法,在注释中,可以翻回去看一下。大 O 表示法仅仅是一种粗略的分析模型,是一种估算帮助我们短时间内了解一个算法的执行效率。
对数阶的细节
- 对数阶一般省略底数
常见的复杂度
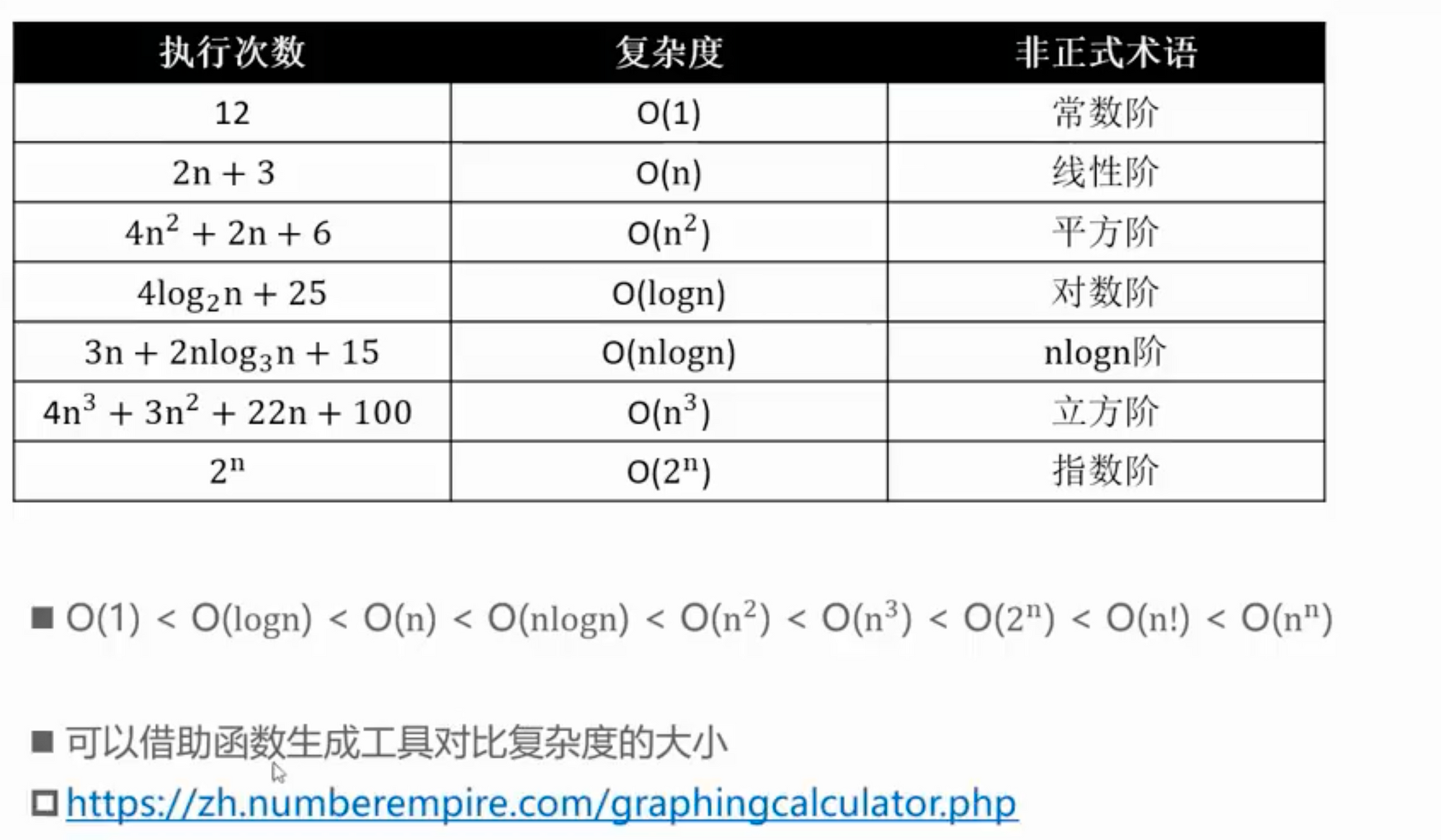
数据规模对比
数据规模较小时候
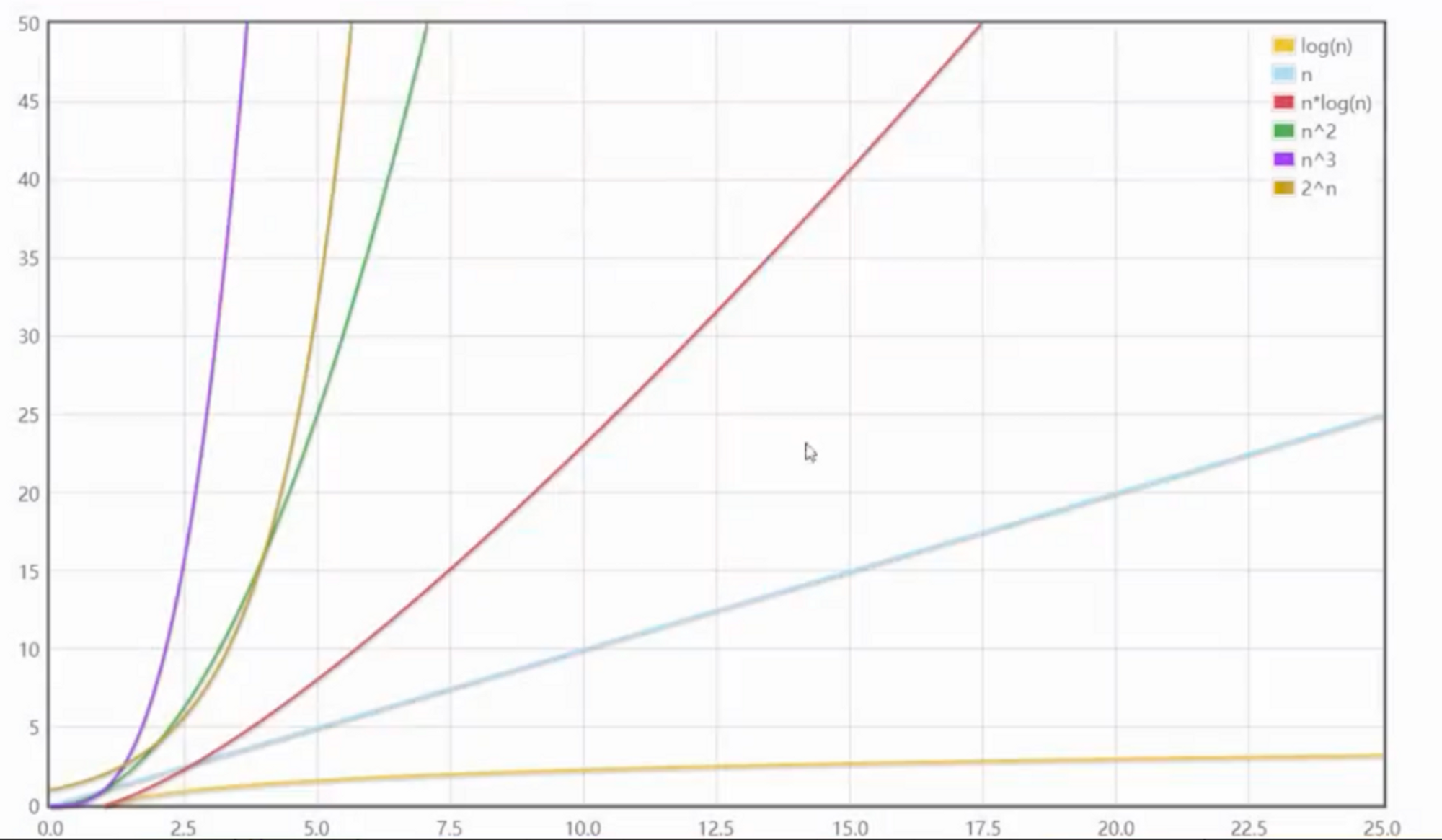
数据规模较大时
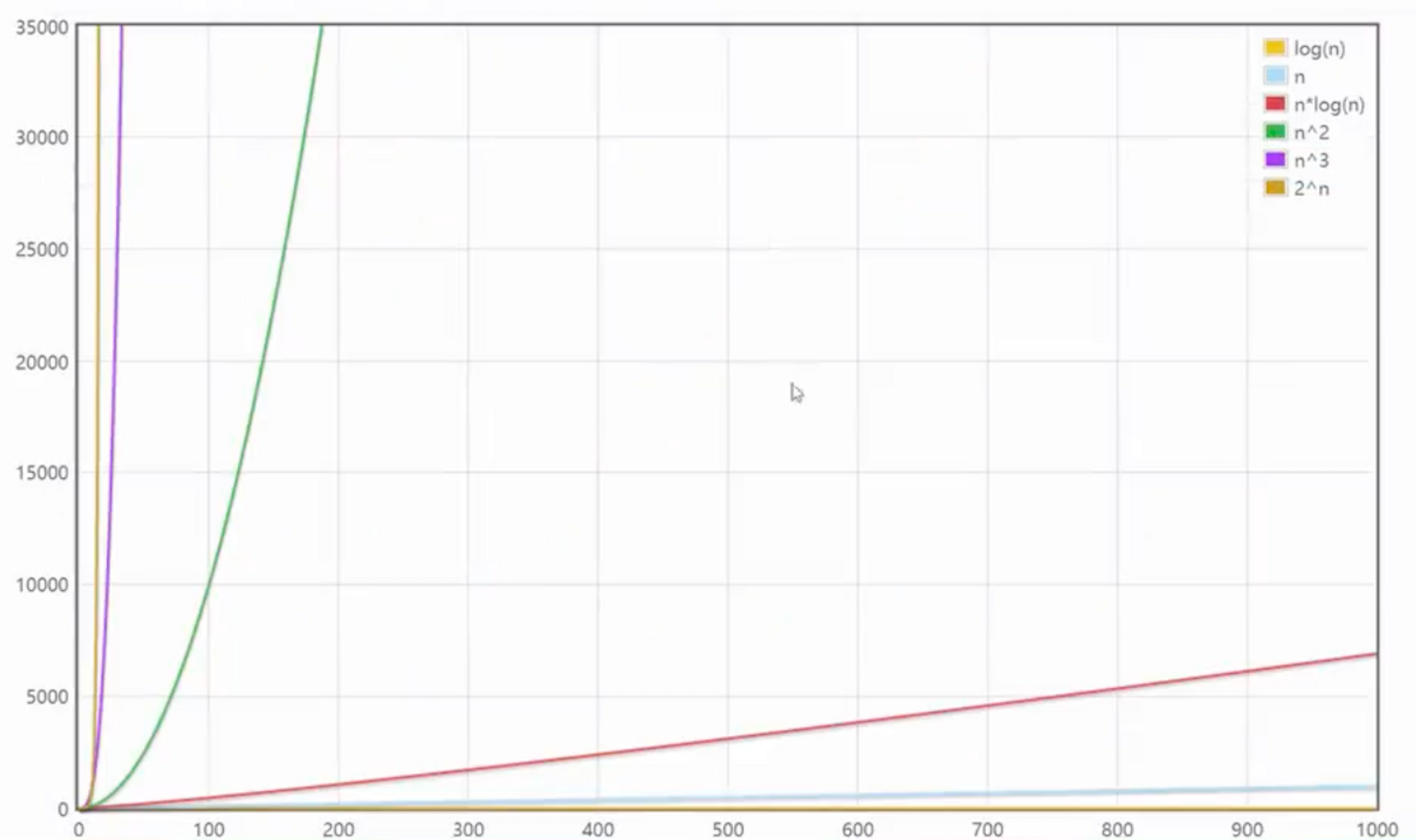
这个对比就已经很明显了。
斐波拉切的时间复杂度
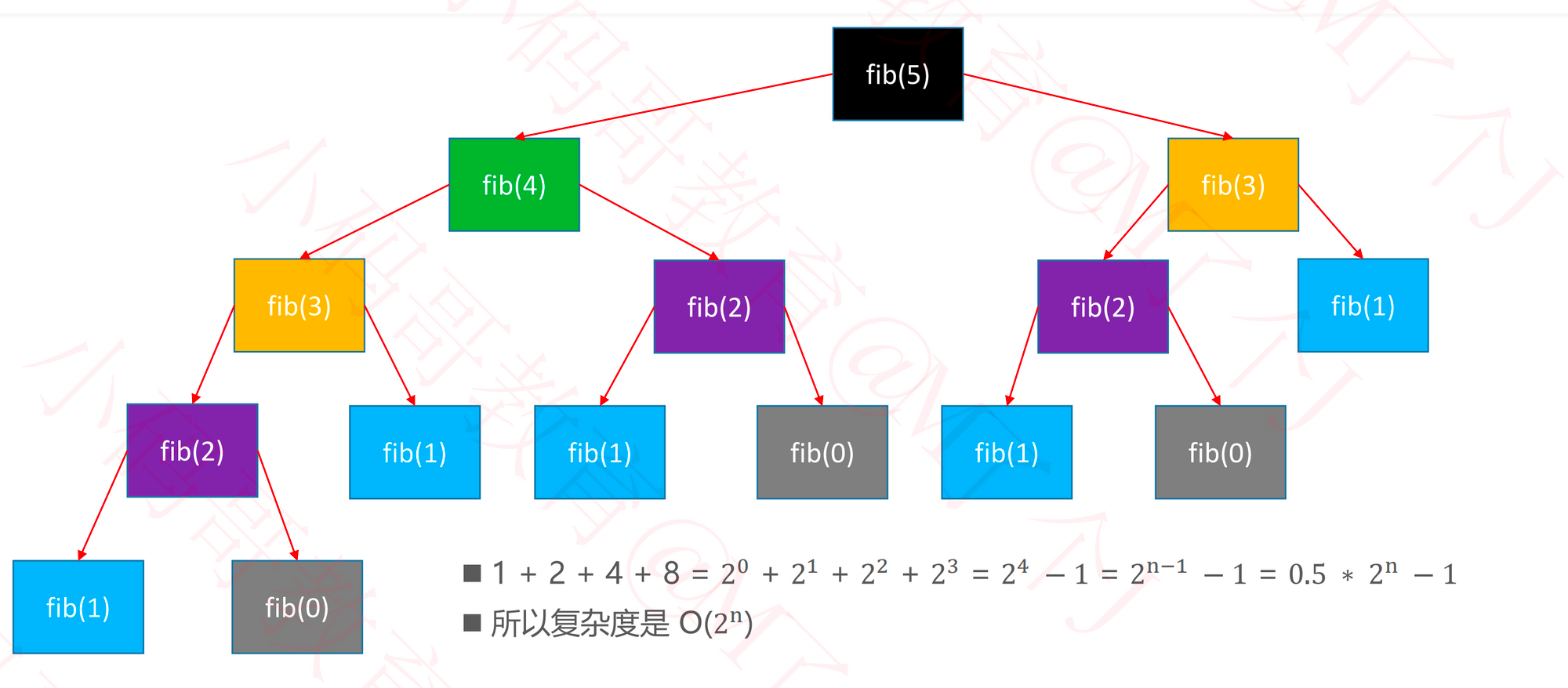
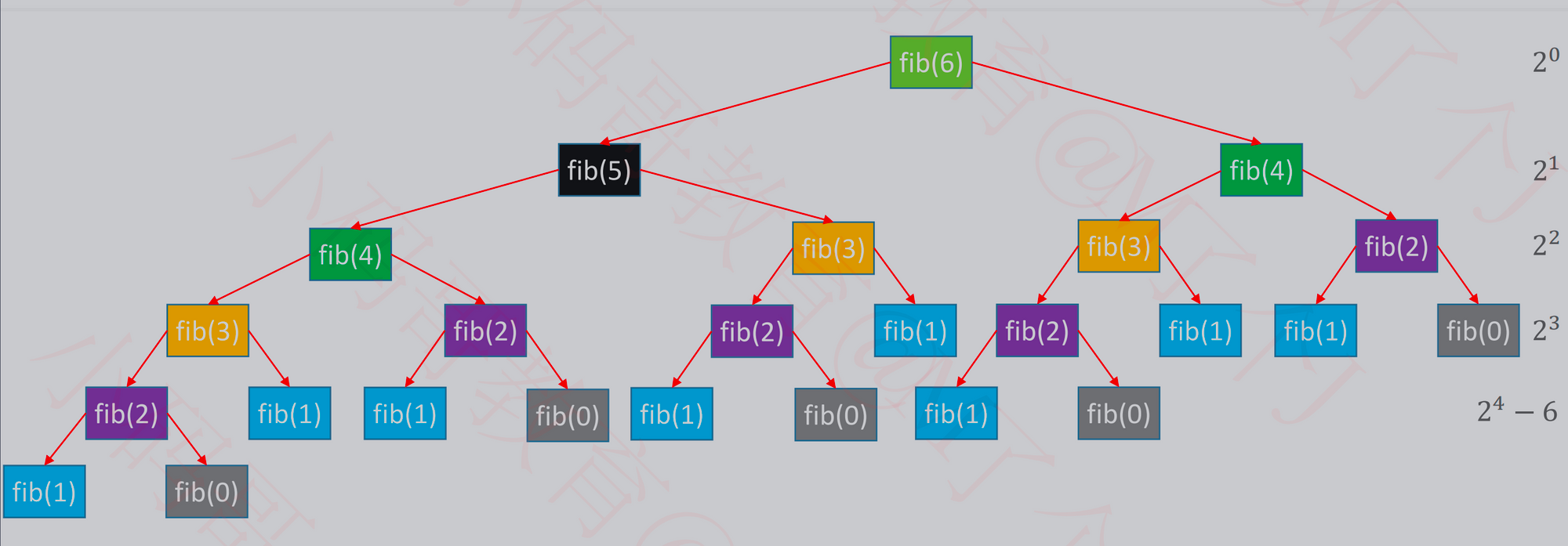
他们的差距有多大?
- 如果是一台 1GHz 的普通计算机,运算速度 10^9 次每秒(n 为 64)
- O(n)大约耗时 6.4 * 18^-18 秒
- O(2^n)大约耗时 584.94 年
- 有时候算法之间的差距,往往比硬件方面的差距还大
算法的优化方向
- 用尽量少的存储空间
- 用尽量少的执行步骤(执行时间)
根据情况:
- 空间换时间
- 时间换空间
多个数据规模的情况
public function void test (int n, int k) {
for (int i = 0; i < n; i++){
System.out.println("test")
}
for (int i = 0; i < k; i++){
System.out.println("test")
}
}这个函数的时间复杂度是由 n 和 k 决定的,O( n + k) 这两个都不能被忽略,因为是两个数据规模
更多的知识
更多的复杂度相关知识,会在后续讲解数据额机构、算法的过程中穿插
- 更好、更坏复杂度
- 均摊复杂度
- 复杂度震荡
- 平均复杂度
