哈夫曼树

哈夫曼编码，又称为霍夫曼编码，它是现代压缩算法的基础，假设要把字符串【ABBBCCCCCCCCDDDDDDEE】转换成二进制编码进行传输，想到的第一种做法可以把他转换成 ASCII 编码（65~69，1000001~1000101）,例如我们现在要传输 ABBB。

ABBB

1000001100001010000101000010

但是有点冗长，如果希望编码更短呢？

可以先约定一下五个字母对对应的二进制。

A  -> 0
B  -> 1
C  -> 10
D  -> 11
E  -> 100

我们依旧传输 ABBB

0111

但是现在有一个问题，我们如何去解释这个二进制呢？因为有的字符是 1 位有的是 2 位有的是三位的。这个二进制中指有 A 是 0 开头的，所以二进制的第一位是 0 我们可以直接解析成 A，但是后面的几位就很难搞了。

按照我们的规则 111 可以被解析为：

• BD
• DB
• BBB

导致这个问题的根本原因是我们的一个字母的编码可以是后一个编码的前缀，所以我们就需要进行约定，每一个编码都不能是后一位的前缀。所以我们先规定，所有字母都用三位:

一共二十个字母，转换成 60 个二进制位.

如果使用哈夫曼编码，可以压缩至 41 个二进制位，约为原来长度的 68.3%。相当于压缩了30%。

哈夫曼树

先计算出每个字母的出现频率（权值，这里直接用出现次数），【ABBBCCCCCCCCDDDDDDEE】。

利用这些权值，构建一颗哈夫曼树（又称为霍夫曼树、最优二叉树）。

如何构建一颗哈夫曼树呢？假设有 n 个权值。

1. 以权值作为根节点构建 n 颗二叉树，组成森林
2. 在森林中选出 2 个根节点最小的树合并，作为一颗新树的左右子树，且新树的根节点为其左右子树根节点之和。
3. 从森林中删除刚刚选取的 2 颗树，并将新树加入森林
4. 重复 2、3步骤，直到森林只剩一棵树为止，该树即为哈夫曼树。

根据规则，我们来构建哈夫曼树,构建过程如下图

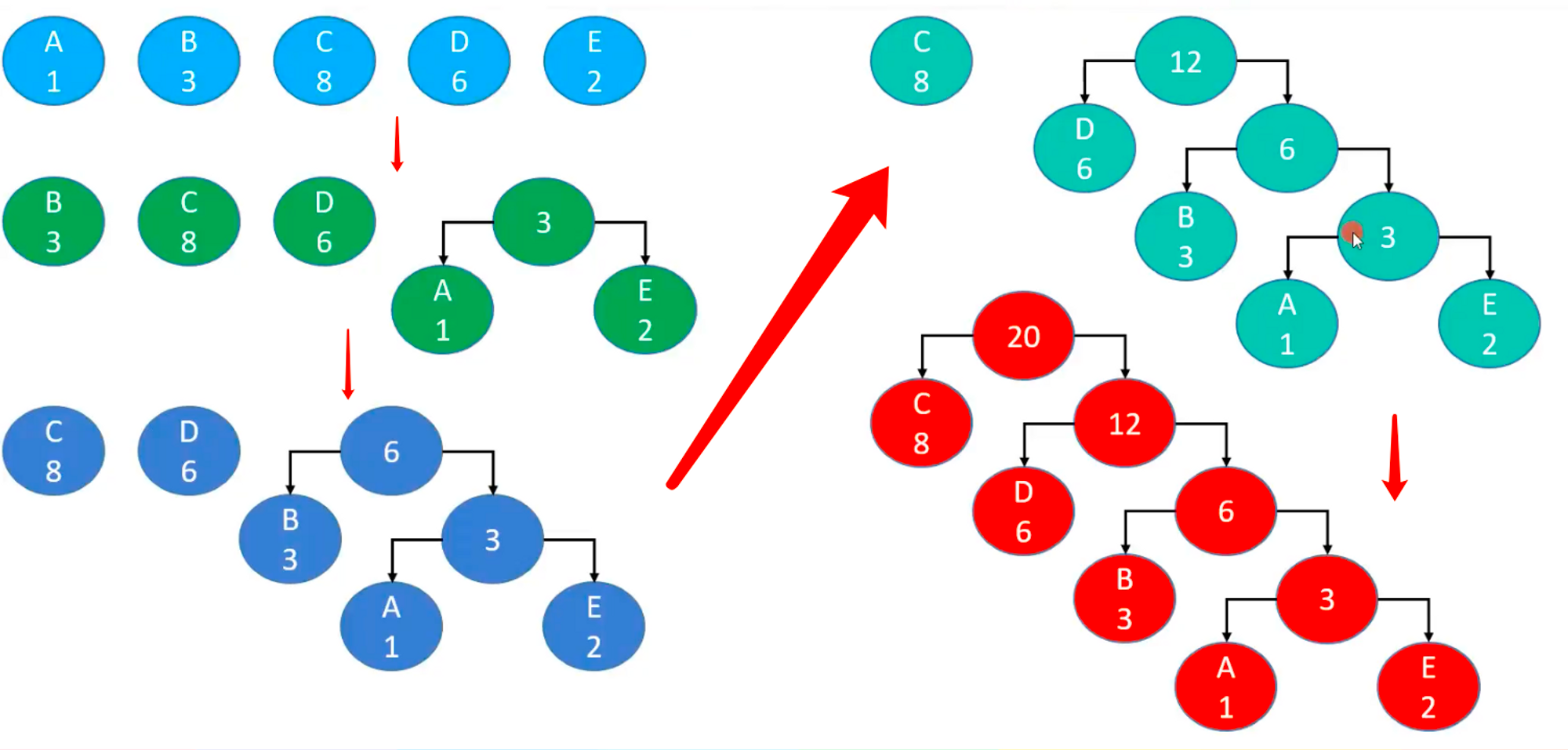
构建哈夫曼编码

以 left 为 0，right 为 1，可以得出 5 个字母对应的哈夫曼编 码

【ABBBCCCCCCCCDDDDDDEE】 的哈夫曼编码是:

11101101101100000000001010101010101111

现在还有一个问题，这个哈夫曼编码传递过去对方能解析吗，我们之前说要对齐编码长度，方便解析，可是在这里长度是不一样的。

哈夫曼的编码有一个特点，那就是的编码都不是其他编码的前缀，结合这一特点，我们就可以注意解析二进制了例如步骤如下：

1. 我们先读去第一个 1 这样就可以将 C 排除了
2. 继续读取，数据变成了 11，这样就把 D 给排除了
3. 继续读取，数据变成了 111 这样就剩下了两个选择，A，E
4. 继续读取，数据编程了 1110 这样就确定了是 A

以此类推就可以解码出所有的字符了。

在哈夫曼中出现次数最多的字符，编码是最短的，在上面的字符串中，C 出现的次数最多，所以它的编码就是 0，出现的最少的字符，编码就是最长的，这样一来，哈夫曼编码出现的二进制天然就是最短的，这样一来就构成了任何一个编码都不是另外编码的前缀。

总结

• n 个权值构建出来的哈夫曼树拥有 n 个子叶子节点
• 每个哈夫曼编码都不是另一个哈夫曼编码的前缀，说白了路径的长短，就是编码的长短，再结合上每个字符其实都是在叶子节点上，这就不可能是其他叶子节点的前缀，因为如果是前缀，需要满足两个节点的关系为父子节点才可以。
• 哈夫曼是带全路径长度最短的树，权值较大的节点离根节点较近
• 带权路径长度：书中所有的叶子结点的权值乘上其道根节点的路径长度。与最终的哈夫曼编码总长度成正比关系